概率
贝叶斯
贝叶斯公式
$$p(Y|X)=\\frac{p(X|Y)p(Y)}{p(X)}$$先验:$p(Y)$,后验:$p(Y|X)$,似然:$p(X|Y)$
$p(X)$可以看做是归一化的量,也可以写成
$$\\int\_Y P(X|Y)p(Y)\\mathrm{d}Y$$极大似然估计,极大后验估计可以看这个。
期望与方差
条件期望
$$E(X|Y=y)=\\sum\_{x\\in \\mathcal X} x P(X=x|Y=y)$$方差与期望的关系
$$\\mathrm{var}(X)=E(X^2)-E(X)^2$$两个变量的协方差:
$$\\mathrm{cov}(X,Y)=E\_{x,y}\[(X-E(X))(Y-E(Y))\]$$协方差反映两个变量的相关程度,正相关则协方差为正,独立则协方为零。
两个向量$\bm X=(X_1,\cdots,X_n)^T,\bm Y=(Y_1,\cdots,Y_n)^T$的协方差矩阵,
$$\\mathrm{cov}(\\bm X,\\bm Y)=\\Big(\\mathrm{cov}(X\_i,Y\_j)\\Big)\_{n\\times n}$$正态分布
参数为$\mu,\sigma$的正态分布的密度函数,
$$N(x|\\mu,\\sigma^2)=\\frac{1}{\\sqrt{2\\pi}\\sigma}\\exp\\left(-\\frac{1}{2\\sigma^2}(x-\\mu)^2\\right)$$正态分布均值为$\mu$,方差为$\sigma^2$。
高维正态分布
$\bm x$是一个$D$维向量,$\bm \mu$是均值,$\bm \Sigma$是协方差矩阵,密度函数如下
$$N(\\bm x|\\bm \\mu,\\bm \\Sigma)=\\frac{1}{(2\\pi)^{D/2}}\\frac{1}{|\\bm \\Sigma|^{1/2}}\\exp\\left(-\\frac{1}{2}(\\bm x-\\bm \\mu)\\bm \\Sigma^{-1}(\\bm x-\\bm \\mu)\\right)$$正态分布的极大似然解
假设我们对一个变量$x$有$n$次独立的观察$\bm x=(x_1,\cdots,x_n)$,极大似然就是要最大化
$$p(\\bm x|\\mu,\\sigma^2)=\\prod\_{i=1}^n N(x\_n|\\mu,\\sigma^2)$$取对数,
$$\\ln p(\\bm x|\\mu,\\sigma^2)=-\\frac{1}{2\\sigma^2}\\sum\_{i=1}^n(x\_i-\\mu)^2-\\frac{n}{2}\\ln \\sigma^2-\\frac{n}{2}\\ln(2\\pi)$$不难解得最值点为
$$\\mu\_{ML}=\\frac{1}{n}\\sum\_{i=1}^n x\_i\\qquad\\sigma^2\_{ML}=\\frac{1}{n}\\sum\_{i=1}^n(x\_i-\\mu\_{ML})^2$$信息论
自信息
$$I(A)=-\\log P(A)$$事件$A$发生的概率越大,那么自信息就越小。
自信息也称信息量
香农熵
随机变量$X$的香农熵就是其自信息的期望,即
$$H(X)=E\_{x\\sim P}\[I(x)\]=-E\_{x\\sim P}\[\\log P(x)\]=\\int -P(x)\\log P(x)\\mathrm{d} x$$$x\sim P$指按概率密度函数$P(x)$计算期望。
若对数的底数取为$2$,那么香农熵就是对$X$进行哈夫曼编码的期望长度。
KL散度
KL散度可以衡量两个分布$P(x)$和$Q(x)$的相似程度
$$D\_{KL}(P||Q)=E\_{x\\sim P}\\left\[\\log\\frac{P(x)}{Q(x)}\\right\]=E\_{x\\sim P}\[\\log P(x)-\\log Q(x)\]$$KL散度又称相对熵。KL散度是非负的,且是一种不对称的衡量。
KL散度的非负性
(吉布斯不等式)若$\sum_{i=1}^n p_i=\sum_{i=1}^n q_i=1$,且$p_i,q_i\in (0,1]$,则有
$$-\\sum\_{i=1}^n p\_i\\log p\_i\\le -\\sum\_{i=1}p\_i\\log q\_i$$等号成立当且仅当$p_i=q_i$。
证明:
$\log_a x$是$\ln x$的常数倍,不妨只考虑$\ln$的情况,由于$\ln x\le x-1$,
$$\\sum\_{i=1}^n p\_i\\ln\\left(\\frac{q\_i}{p\_i}\\right)\\le \\sum\_{i=1}^n p\_i\\left(\\frac{p\_i}{q\_i}-1\\right)=0$$证毕
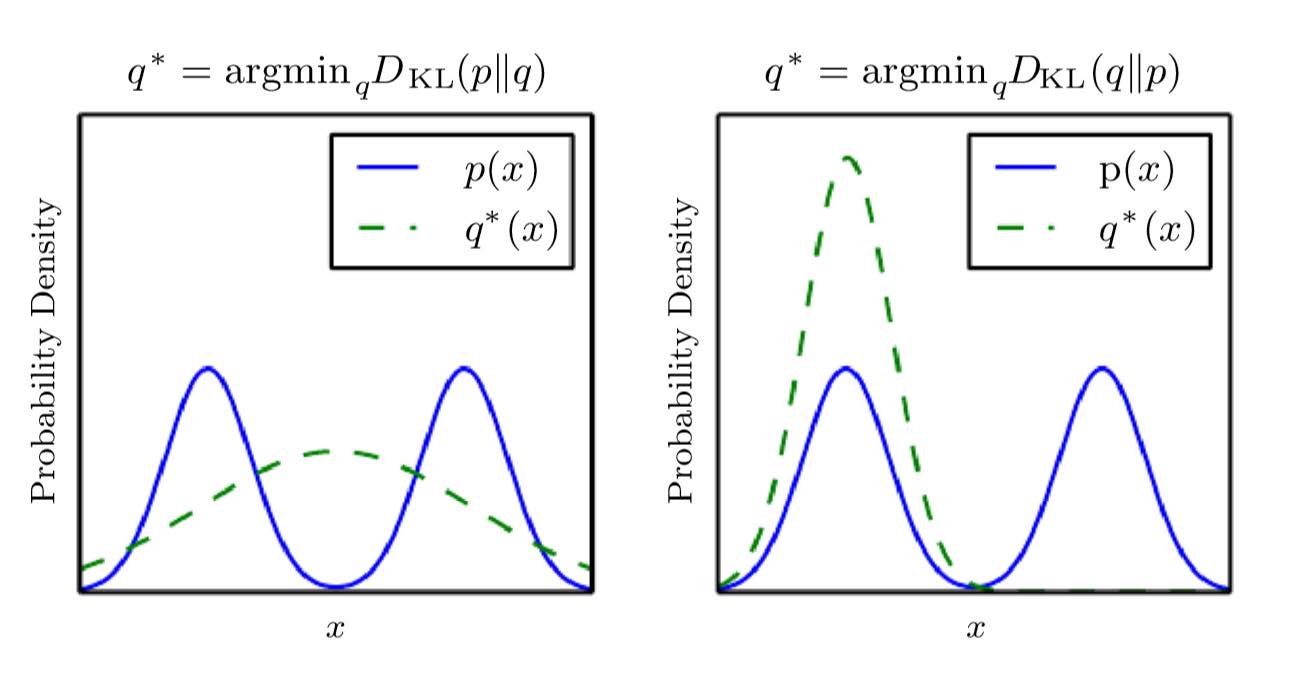
KL散度的不对称性
注意到$D_{KL}(P||Q)$与$D_{KL}(Q||P)$并不相等。
假设给定分布$P$,需要求一个服从特定分布(例如正态分布)的$Q$,使得$P$和$Q$尽量“相近”,那么就有两种方式:
-
$Q^* = \argmin_Q D_{KL}(P||Q)$
-
$Q^* = \argmin_Q D_{KL}(Q||P)$
第一种偏向于“$P$高$Q$高”,第二种倾向于“$P$低$Q$低”,如图。
交叉熵
$$H(P,Q)=-E\_{x\\sim P}\[\\log Q(x)\]$$可以注意到交叉熵就是香农熵和KL散度的和,即
$$H(P,Q)=H(P)+D\_{KL}(P||Q)$$交叉熵表示基于分布$Q$(往往是人们猜测or估计的)对一个服从分布$P$(往往是真实但不可知的)的变量进行编码的期望长度。
那么KL散度就可以理解为用错误分布进行编码耗费的额外长度。