概率

贝叶斯

贝叶斯公式

$$p(Y|X)=\frac{p(X|Y)p(Y)}{p(X)}$$

先验：$p(Y)$，后验：$p(Y|X)$，似然：$p(X|Y)$

$p(X)$可以看做是归一化的量，也可以写成

$$\int_Y P(X|Y)p(Y)\mathrm{d}Y$$

极大似然估计，极大后验估计可以看这个。

期望与方差

条件期望

$$E(X|Y=y)=\sum_{x\in \mathcal X} x P(X=x|Y=y)$$

方差与期望的关系

$$\mathrm{var}(X)=E(X^2)-E(X)^2$$

两个变量的协方差：

$$\mathrm{cov}(X,Y)=E_{x,y}[(X-E(X))(Y-E(Y))]$$

协方差反映两个变量的相关程度，正相关则协方差为正，独立则协方为零。

两个向量$\bm X=(X_1,\cdots,X_n)^T,\bm Y=(Y_1,\cdots,Y_n)^T$的协方差矩阵，

$$\mathrm{cov}(\bm X,\bm Y)=\Big(\mathrm{cov}(X_i,Y_j)\Big)_{n\times n}$$

正态分布

参数为$\mu,\sigma$的正态分布的密度函数，

$$N(x|\mu,\sigma^2)=\frac{1}{\sqrt{2\pi}\sigma}\exp\left(-\frac{1}{2\sigma^2}(x-\mu)^2\right)$$

正态分布均值为$\mu$，方差为$\sigma^2$。

高维正态分布

$\bm x$是一个$D$维向量，$\bm \mu$是均值，$\bm \Sigma$是协方差矩阵，密度函数如下

$$N(\bm x|\bm \mu,\bm \Sigma)=\frac{1}{(2\pi)^{D/2}}\frac{1}{|\bm \Sigma|^{1/2}}\exp\left(-\frac{1}{2}(\bm x-\bm \mu)\bm \Sigma^{-1}(\bm x-\bm \mu)\right)$$

正态分布的极大似然解

假设我们对一个变量$x$有$n$次独立的观察$\bm x=(x_1,\cdots,x_n)$，极大似然就是要最大化

$$p(\bm x|\mu,\sigma^2)=\prod_{i=1}^n N(x_n|\mu,\sigma^2)$$

取对数，

$$\ln p(\bm x|\mu,\sigma^2)=-\frac{1}{2\sigma^2}\sum_{i=1}^n(x_i-\mu)^2-\frac{n}{2}\ln \sigma^2-\frac{n}{2}\ln(2\pi)$$

不难解得最值点为

$$\mu_{ML}=\frac{1}{n}\sum_{i=1}^n x_i\qquad\sigma^2_{ML}=\frac{1}{n}\sum_{i=1}^n(x_i-\mu_{ML})^2$$

信息论

自信息

$$I(A)=-\log P(A)$$

事件$A$发生的概率越大，那么自信息就越小。

自信息也称信息量

香农熵

随机变量$X$的香农熵就是其自信息的期望，即

$$H(X)=E_{x\sim P}[I(x)]=-E_{x\sim P}[\log P(x)]=\int -P(x)\log P(x)\mathrm{d} x$$

$x\sim P$指按概率密度函数$P(x)$计算期望。

若对数的底数取为$2$，那么香农熵就是对$X$进行哈夫曼编码的期望长度。

KL散度

KL散度可以衡量两个分布$P(x)$和$Q(x)$的相似程度

$$D_{KL}(P||Q)=E_{x\sim P}\left[\log\frac{P(x)}{Q(x)}\right]=E_{x\sim P}[\log P(x)-\log Q(x)]$$

KL散度又称相对熵。KL散度是非负的，且是一种不对称的衡量。

KL散度的非负性

（吉布斯不等式）若$\sum_{i=1}^n p_i=\sum_{i=1}^n q_i=1$，且$p_i,q_i\in (0,1]$，则有$$-\sum_{i=1}^n p_i\log p_i\le -\sum_{i=1}p_i\log q_i$$等号成立当且仅当$p_i=q_i$。

证明：

$\log_a x$是$\ln x$的常数倍，不妨只考虑$\ln$的情况，由于$\ln x\le x-1$，

$$\sum_{i=1}^n p_i\ln\left(\frac{q_i}{p_i}\right)\le \sum_{i=1}^n p_i\left(\frac{p_i}{q_i}-1\right)=0$$

证毕

KL散度的不对称性

注意到$D_{KL}(P||Q)$与$D_{KL}(Q||P)$并不相等。

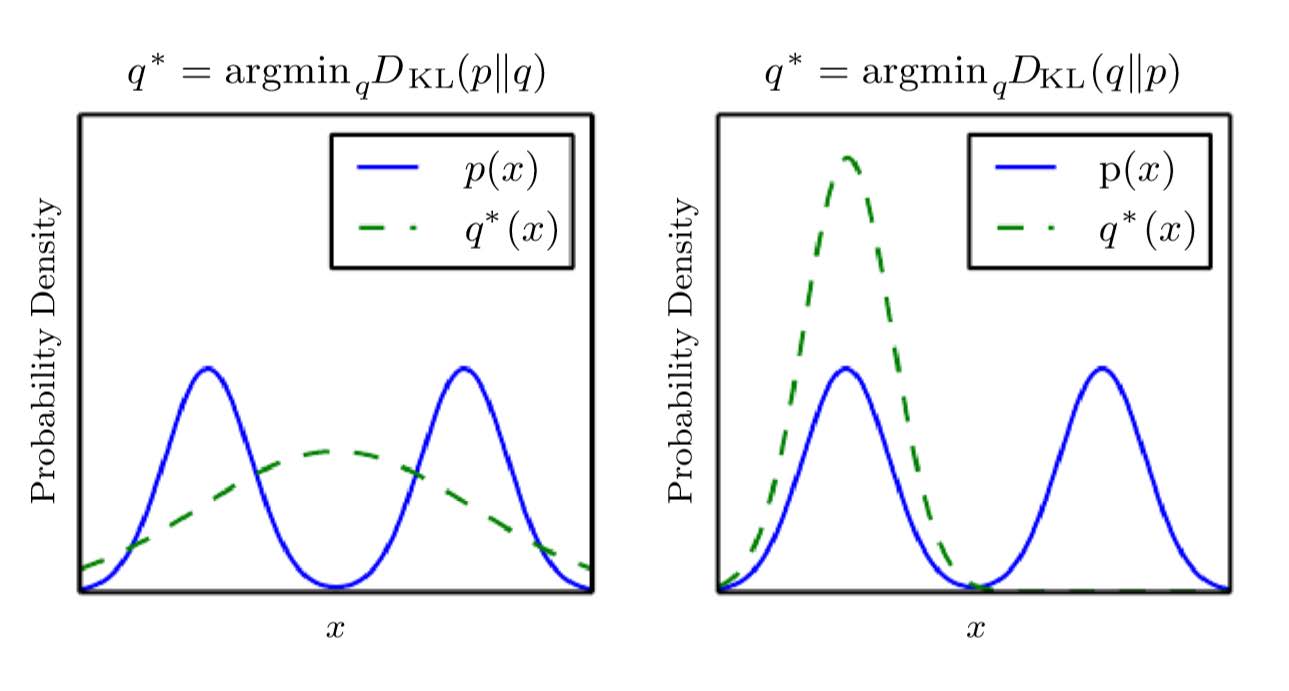
假设给定分布$P$，需要求一个服从特定分布（例如正态分布）的$Q$，使得$P$和$Q$尽量“相近”，那么就有两种方式：

1. $Q^* = \argmin_Q D_{KL}(P||Q)$

2. $Q^* = \argmin_Q D_{KL}(Q||P)$

第一种偏向于“$P$高$Q$高”，第二种倾向于“$P$低$Q$低”，如图。

交叉熵

$$H(P,Q)=-E_{x\sim P}[\log Q(x)]$$

可以注意到交叉熵就是香农熵和KL散度的和，即

$$H(P,Q)=H(P)+D_{KL}(P||Q)$$

交叉熵表示基于分布$Q$（往往是人们猜测or估计的）对一个服从分布$P$（往往是真实但不可知的）的变量进行编码的期望长度。

那么KL散度就可以理解为用错误分布进行编码耗费的额外长度。

如何通俗的解释交叉熵与相对熵？ – erwin的回答 – 知乎