Link: The Logic of Computer Programming
Four aspect:
- correctness
- termination
- transformation
- development
Program A:

Partial Correctness
totally correct: if we execute Program A on any input satisfying the input assertion, the program will halt with output satisfying the output assertion.
partial correctness: assume halts
intermediate assertion: more information about the relation of variables at the middle of program (so it helps to know more about the program than just the input and output assertions)
verification: prove the implication relations between all adjacent assertions.
Difficulties of this method:
a knowledge of the subject domain of the program (e.g., the properties of integers or the laws of physics) is required both for finding the intermediate assertions and proving the verification conditions.
A more recent method:
– subgoal assertion: relate the intermediate values of the program variables with their ultimate values when the program halts.
From a theoretical point of view, the invariant-assertion method and the subgoal-assertion method are equivalent in
power.
Then, the author demonstrated the parital correctness of Program A.
invariant statement: $\{P\}F\{Q\}$, means that if the input assertions $P$ holds, after execute the program segment $F$, the output assertions $P$ holds as well.
Rules of inference:
- Assignment Rule

- Conditional Rule

- While Rule

- Concatenation Rule

Termination
- a well-founded set and a order on in
- or introduce a counter to bound the loop times
Computational induction: induction on the number of steps in the computataion.
Sturctral induction: induction independent of the computation.
Total Correctness
intermittent assertion
Correctness of Recursive Program
Also partial correctness + termination.
Program Transformation
Equivalence-preserving transformations: totaly equivalent to the original one. (such as elimination of common subexpressions )
Correctness preserving transformations: yields a program that is guaranteed to be correct(keep the input-output assertions satisfied), but not necessarily equivalent to the original program.
Program Development
From specifications to program
A example of developing gcd from specifications to program is given. Then some of basic principles is concluded:
- Transformation Rules: the rules try to replace the nonprimitive constructs of the specification by primitive constructs of programming language.
- Conditional Introduction: when a transformation requires a condition that cannot be proved or disproved, a case analysis may help (e.g.,at Goal 5, try to discuss whether $y\ge x$), and yielding a conditional expression in the ultimate program.
- Recursion Introduction: when a subgoal is an instance of any higher level subgoal, a recursive call can be introduced. (e.g. )
If additional knowledge is known
If some properties of gcd are known (like properties shown in the figure), we can facilitate the process by admitting the use of these properties.
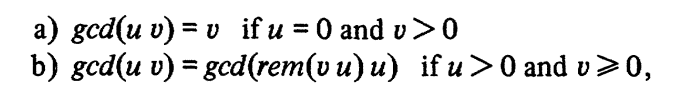
Then some additional principles are concluded:
- Variable Introduction: introduce new program variables.
- Iteration Introduction: If a goal is a conjunction of several conditions, attempt to introduce an iterative loop whose exit test is one of the conditions and whose invariant assertion is the conjuction of the others.
And some other program development techniques:
- Generalization: In deriving a recusive program, try to generalize the program’s specification to make recusive call satisfy a desired subgoal; In constructing an iteraive program, try to generalize the invariant assertion.
- Simultaneous Goals: extend the program, protecting the first condition meanwhile, to achieve other conditions. (similar to achieve goals one by one)
- Efficiency: decide the choice of transformations.
Develop a program by taking advantage of developed programs
A example of computing lcm extended form gcd program is shown.
Although it is straight forward to use the properties that$$lcm(x_0,y_0)=x_0\cdot y_0 / gcd (x_0,y_0)$$
the given example successfully completes the extention only use addition and subtraction.
At the end of the paper, the author also discussed program adaptation and pointed out that program debugging is a special case of adaptation.

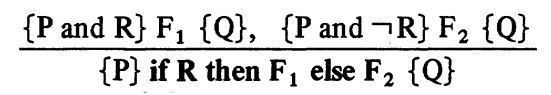
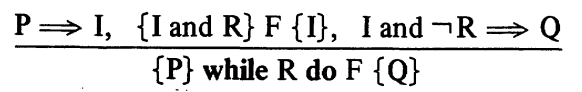
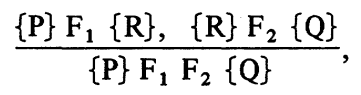
发表回复